Yesterday one of my student came to me and asked why we use Liner Regression anymore while we have Neural Network around. I thought for a beginners who did not go through basics in detail for Neural Network, its better to give some information here.

Yes, Neural network is not a simple linear regression. A neural network is a machine learning model that is inspired by the structure and function of the human brain and is used for a wide range of tasks such as image classification, natural language processing, and speech recognition. Linear regression, on the other hand, is a statistical method for finding the best-fitting straight line through a set of data points. While linear regression can be used as a building block for neural networks, it is just one of many different types of layers and functions that can be used in a neural network.

Linear regression can be used as a building block in a neural network, specifically in a fully connected layer, also known as a dense layer. In this context, a dense layer with a linear activation function can be seen as a linear regression model.

A neural network is a machine learning model that consists of layers of interconnected nodes, called neurons. These layers are organized into an input layer, one or more hidden layers, and an output layer. The input layer receives the raw data and passes it through the network, where it is processed by the hidden layers before reaching the output layer. Each layer is composed of multiple neurons, and each neuron receives input from the neurons of the previous layer, performs a calculation on that input, and sends the output to the next layer.

A dense layer, also known as a fully connected layer, is a type of layer where each neuron receives input from all the neurons of the previous layer. In other words, all neurons in one layer are connected to all neurons in the next layer. Each neuron in a dense layer performs a linear combination of the inputs using a set of weights and biases. This linear combination can be represented by the equation y = Wx + b, where y is the output, x is the input, W is the weights matrix, and b is the bias.

This equation is similar to the equation of a line in linear regression y = mx + b, which indicates that linear regression can be seen as a single dense layer with a linear activation function. In this context, the weights are the slope of the line, the bias is the y-intercept, and the inputs are the x values. So, a dense layer with a linear activation function can be seen as a linear regression model.

It’s important to note that while a single dense layer with a linear activation function can be seen as a linear regression model, neural networks are more powerful than linear regression because they can model complex and non-linear relationships between inputs and outputs. This is achieved by stacking multiple layers and using non-linear activation functions.

Lets See an Example to make it more clear

let’s say we have a dataset of a publicly available dataset that can be used for linear regression is the Boston Housing dataset. It is a dataset of housing prices in the Boston area, including information such as crime rate, property tax rate, and the number of rooms in each house.

data_url = “http://lib.stat.cmu.edu/datasets/boston“

Here’s an example of how to load the Boston Housing dataset in Python using the scikit-learn library:

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split

# Load the Boston Housing dataset
boston = load_boston()

# Split the data into input (X) and output (y)
X = boston.data
y = boston.target

# Split the data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

This dataset contains 506 samples and 13 features, you can use any of these features as input for the linear regression model, for example, you can use the number of rooms feature as the input and the target is the median value of owner-occupied homes in $1000’s. To show Simple Liner Regression, I will use only one neuron.

Here is how to define, compile and train model:

from keras.layers import Input, Dense
from keras.models import Model

# Create an input layer with 1 neuron
inputs = Input(shape=(1,))

# Create a dense layer with 1 neuron and linear activation function
predictions = Dense(1, activation='linear')(inputs)

# Create a model from the input and predictions layers
model = Model(inputs=inputs, outputs=predictions)

# Compile the model
model.compile(optimizer='sgd', loss='mean_squared_error')

# Train the model on the training data
model.fit(X_train[:,5], y_train, epochs=10)

In this example, we’re using the functional API of Keras to create a model. We’re creating an input layer with 1 neuron, which represents the number of rooms in the house. Then, we’re creating a dense layer with 1 neuron and a linear activation function, which represents the median value of owner-occupied homes in $1000’s. The dense layer with 1 neuron is the output layer, and the activation function is linear which means this layer is doing the linear regression.

We’re then compiling the model by specifying the optimizer and the loss function. We’re using the stochastic gradient descent optimizer and mean squared error as the loss function.

Finally, we’re training the model on the training data by calling the fit() method and passing in the training data and the number of epochs.

Once the model is trained, you can use the predict() method to make predictions on new data and evaluate the model on the test data to see how well it performs on unseen data.

It’s important to note that you can use other features from the Boston Housing dataset instead of the number of rooms and you can also try different architectures and optimizers to improve the performance of the model.

# Make predictions on the test data
y_pred = model.predict(X_test[:,5])

# Evaluate the model on the test data
test_loss = model.evaluate(X_test[:,5], y_test)
print('Test loss:', test_loss)

As you can see, this is a simple linear regression model, it’s a single layer neural network, where the input layer receives the square footage of the house, and the output layer makes the prediction of the house’s price. The dense layer with 1 neuron and linear activation function is responsible for making the final prediction based on the input square footage. The model is trained using the provided dataset and the mean squared error as the loss function.

Lets Visualize it

import matplotlib.pyplot as plt

# Plot the predicted values versus the actual values
plt.scatter(y_test, y_pred)
plt.xlabel('Actual values')
plt.ylabel('Predicted values')
plt.show()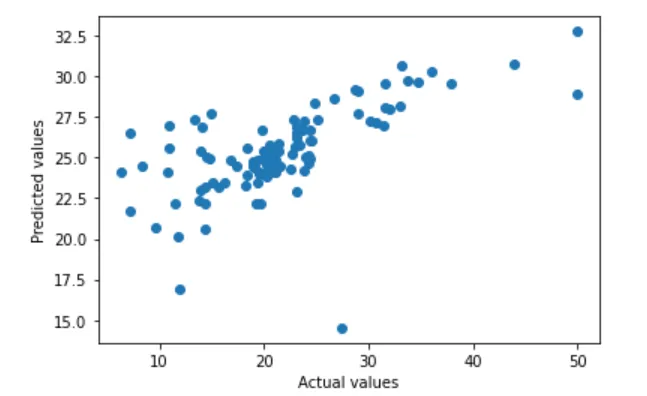

This will create a scatter plot where the x-axis represents the actual values and the y-axis represents the predicted values. Ideally, the points on the plot should be close to the diagonal line, this indicates that the model is making accurate predictions.

It’s important to keep in mind that the performance of the model will be affected by the quality and completeness of the data, so you should evaluate the model on a separate validation set or use cross-validation techniques to get a more accurate estimate of its performance.

So, When to use Liner Regression and when to not?

When to use Linear Regression:

• When the relationship between the input features and the output is linear.
• When you want to make a simple and interpretable model.
• When you want to make predictions based on a small number of input features.
• When you have a large amount of data, linear regression can handle a large number of data points.

When not to use Linear Regression:

• When the relationship between the input features and the output is non-linear. In this case, you may need to use more advanced models such as polynomial regression or decision trees.
• When you want to make predictions based on a large number of input features. In this case, you may need to use more advanced models such as Random Forest or Neural Networks.
• When the data is noisy and not well-behaved, linear regression may not be the best choice as it may not be able to capture the underlying pattern in the data.
• When the data is not independent and identically distributed. Linear regression assumes that the observations in the dataset are independent and identically distributed, if not it may not be the best choice.

Summary:

Linear regression is a simple yet powerful technique that is widely used in many fields, including finance, economics, and statistics. In a neural network context, a linear regression layer can be used as a building block for more complex models, such as multi-layer perceptrons (MLPs) and convolutional neural networks (CNNs).

Linear regression can be used to make predictions based on a single input feature or multiple input features. In the examples I provided, I used a single input feature (number of rooms) to make predictions, but you can use multiple input features to make more accurate predictions. For example, you can use the number of rooms, the crime rate, and the property tax rate as input features to make predictions about housing prices.

One important thing to keep in mind when using linear regression in a neural network context is that the input features should be preprocessed and scaled before being used as input to the model. This is because the activation function of the linear regression layer is sensitive to the scale of the input features. Scaling the input features ensures that the model can converge faster and produce more accurate predictions.

Finally, it’s important to note that linear regression is a linear model, which means it can only capture linear relationships between the input features and the output. For more complex and non-linear relationships, you may need to use more advanced models such as polynomial regression or decision trees.

— — — — — — — — — — — — — — — — — — — — — — — — — — — — — — — —

#Linear Regression
#Machine Learning
#AI
#Artificial Intelligence
#Data Science